Cho tứ giác nội tiếp ABCD có AC vuông góc với BD tại H. Gọi
Câu hỏi và phương pháp giải
Nhận biếtCho tứ giác nội tiếp ABCD có AC vuông góc với BD tại H. Gọi M là điểm trên cạnh AB sao cho AM = 
AB và N là trung điểm của HC. Chứng minh rằng đường thẳng DN vuông góc với đường thẳng MH.
Đáp án đúng: B
Lời giải của Luyện Tập 247
Cách giải nhanh bài tập này
Trên tia HD lấy điểm E sao cho HE=HB.Gọi K là trung điểm HE. F là giao điểm của CE và AD.
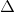CBE có CH vừa là đường cao vừa là đường trung tuyến (CH vuông góc với BE, HE =HB) =>
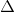CBE cân tại C.
=> CH là tia phân giác của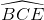 
=> 
=
.
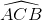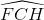Mà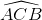 
=
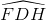(hai góc nội tiếp cùng chắn cung AB)
Ta có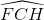 
=
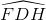=> Tứ giác DFHC nội tiếp
=>
=
= 
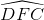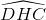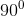
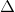HEC có HN=NC,KH=KE
=> KN là đường trung bình của tam giác HEC
=> KN//CE
Mà CE vuông góc với AD (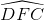
= 
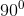) nên KN vuông góc với AD
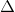AND có DH, KN là 2 đường cao cắt nhau tại K=> K là trực tâm tam giác AND=> AK vuông góc DN
ABK có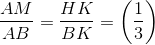 
=> AK // MH (định lí Talet đảo )
Ta có AK//MH và AK vuông góc DN. Vậy DN vuông góc MH.