Một vật dao động điều hòa với phương trình x = 4cos pi

Lời giải của Luyện Tập 247

Phương pháp giải:

Chu kì dao động: (T = dfrac{{2pi }}{omega })

Sử dụng vòng tròn lượng giác và công thức (Delta t = dfrac{{Delta varphi }}{omega })

Giải chi tiết:

Chu kì dao động của vật là: (T = dfrac{{2pi }}{omega } = dfrac{{2pi }}{pi } = 2,,left( s right))

Trong 1 chu kì, vật đi qua vị trí cách vị trí cân bằng (2,,cm) 4 lần 

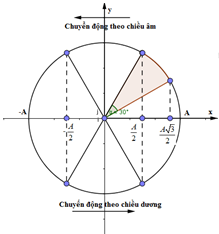
Từ VTLG, ta thấy thời điểm đầu tiên vật đi đến vị trí cách vị trí cân bằng (dfrac{A}{2}) lần đầu tiên, vật quét được góc (dfrac{pi }{6}.)

Vậy áp dụng mối liên hệ giữa góc quét (Delta varphi ) và khoảng thời gian ∆t, ta có:

(Delta varphi  = dfrac{pi }{6} Rightarrow Delta t = dfrac{{Delta varphi }}{omega } = dfrac{{dfrac{pi }{6}}}{{dfrac{{2pi }}{T}}} = dfrac{T}{{12}}{mkern 1mu} )

Thời điểm vật qua vị trí cách VTCB 2 cm lần thứ 5 là:

(t = T + Delta t = T + dfrac{T}{{12}} approx 2,17,,left( s right))

Chọn A.