Bài toán mặt cầu của hình chóp có các cạnh bên bằng nhau

Bài toán mặt cầu của hình chóp có các cạnh bên bằng nhau
Phương pháp giải bài toán mặt cầu của hình chóp
Xét khối chóp $S.ABC$ có $SA=SB=SC.$ Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối chóp $S.ABC$ (Hình chóp đều là một trường hợp đặc biệt của dạng toán này).
Dựng tâm. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC thì ta có $SO\bot \left( ABC \right).$ Trong mặt phẳng $\left( SAO \right)$ dựng đường trung trực của SA cắt SO tại I thì I là tâm mặt cầu ngoại tiếp khối chóp $S.ABC$.
Tính bán kính $R$ của mặt cầu.
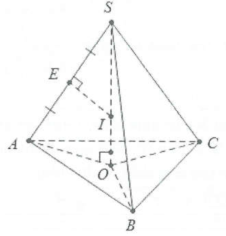
Gọi E là trung điểm của AB.
Hai tam giác vuông SOA và SEI đồng dạng.
Suy ra $\frac{SO}{SE}=\frac{SA}{SI}\Leftrightarrow R=SI=\frac{SE.SA}{SO}=\frac{S{{A}^{2}}}{2SO}.$
Vậy $R=\frac{S{{A}^{2}}}{2SH}.$
Tổng quát: Cho khối chóp $S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ có $S.{{A}_{1}}=S{{A}_{2}}...S{{A}_{n}}=\ell $ và có chiều cao $SO=h$ thì bán kính mặt cầu ngoại tiếp R của khối chóp $S.{{A}_{1}}{{A}_{2}}...{{A}_{n}}$ được tính theo công thức: $R=\frac{{{\ell }^{2}}}{2SO}=\frac{{{\ell }^{2}}}{2h}.$
Bài tập trắc nghiệm của mặt cầu của hình chóp có đáp án chi tiết
| Ví dụ 1: Thể tích khối cầu ngoại tiếp hình chóp tam giác đều $S.ABC$ có $AB=a,SA=a\sqrt{2}$ bằng A. $\frac{4\sqrt{5}\pi {{a}^{3}}}{75}.$ B. $\frac{4\sqrt{15}\pi {{a}^{3}}}{25}.$ C. $\frac{4\sqrt{3}\pi {{a}^{3}}}{25}.$ D. $\frac{4\sqrt{3}\pi {{a}^{3}}}{75}.$ |
Lời giải
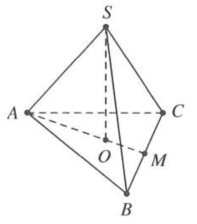
Gọi O là tâm đường tròn ngoại tiếp $\Delta ABC\xrightarrow{{}}SO\bot \left( ABC \right)$
Gọi M là trung điểm của $BC\Rightarrow OA=\frac{2}{3}AM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$
Tam giác SAO vuông tại $O\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\frac{a\sqrt{15}}{3}$
Vậy $SA=a\sqrt{2};SO=\frac{a\sqrt{15}}{3}\xrightarrow{{}}R=\frac{a\sqrt{15}}{5}\Rightarrow V=\frac{4\sqrt{15}\pi {{a}^{3}}}{25}.$
Chọn B.
Mở rộng với bài toán hình chóp tam giác đều. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng a, với giả thiết
| Cạnh bên $SA=b$ thì $R=\frac{\sqrt{3}.{{b}^{2}}}{2\sqrt{3{{b}^{2}}-{{a}^{2}}}}.$ Cạnh bên SA hợp với đáy một góc $\alpha $ thì $R=\frac{\sqrt{3}}{3.\sin 2\alpha }a.$ Mặt bên tạo với mặt đáy một góc $\beta $ thì $R=\frac{\sqrt{3}\left( 4+{{\tan }^{2}}\beta \right)}{12\tan \beta }a.$ Góc $\widehat{SAB}=\varphi $ thì $R=\frac{\sqrt{3}.a}{4\sqrt{-\cos \varphi .\cos 3\varphi }}.$ Góc $\widehat{ASB}=\gamma $ thì $R=\frac{\sqrt{3}.a}{4\sqrt{\sin \frac{\gamma }{2}.\sin \frac{3\gamma }{2}}}.$ |
| Ví dụ 2: Cho hình chóp $S.ABC$ có đáy ABC là tam giác vuông cân tại $A,AB=a\sqrt{2}.$ Các cạnh bên $SA=SB=SC.$ Góc giữa đường thẳng SA và mặt phẳng \[\left( ABC \right)\] bằng ${{45}^{0}}.$ Bán kính mặt cầu ngoại tiếp hình chóp $S.ABC$ bằng A. $\frac{a\sqrt{2}}{4}.$ B. $\frac{a}{2}.$ C. $\frac{a\sqrt{2}}{2}.$ D. $a.$ |
Lời giải
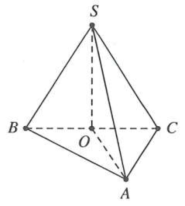
Gọi O là trung điểm $BC\Rightarrow O$ là tâm đường tròn ngoại tiếp $\Delta ABC$
\[\Rightarrow SO\bot \left( ABC \right)\Rightarrow \left( \widehat{SA;\left( ABC \right)} \right)=\widehat{\left( SA;OA \right)}=\widehat{SAO}={{45}^{0}}\]
Tam giác ABC vuông cân tại $A\xrightarrow{{}}BC=AB\sqrt{2}=2a$
Tam giác SAO vuông cân tại $O\xrightarrow{{}}SO=OA=\frac{BC}{2}=a$
Vậy $SO=a;SA=OA\sqrt{2}=a\sqrt{2}\xrightarrow{{}}R=a.$
Chọn D.
| Ví dụ 3: Cho hình chóp đều $S.ABC$ có cạnh đáy bằng 1, khoảng cách từ điểm A đến mặt phẳng $\left( SBC \right)$ bằng $\frac{\sqrt{6}}{4}$. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng A. $\frac{25\pi }{12}.$ B. $\frac{25\pi }{24}.$ C. $\frac{5\pi }{12}.$ D. $\frac{5\pi }{24}.$ |
Lời giải
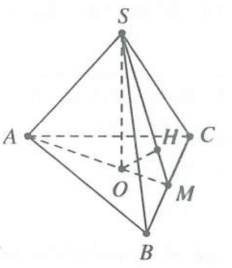
Gọi O là tâm tam giác $ABC,M$ là trung điểm BC
\[\Rightarrow SO\bot \left( ABC \right);OA=\frac{2}{3}AM=\frac{2}{3}.\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3};OM=\frac{1}{2}OA=\frac{\sqrt{3}}{6}\]
Kẻ $OH\bot SM\left( H\in SM \right)\xrightarrow{{}}OH\bot \left( SBC \right)$
Ta có $d\left( A;\left( ABC \right) \right)=3.OH\Rightarrow OH=\frac{\sqrt{6}}{4}:3=\frac{\sqrt{6}}{12}$
Tam giác SMO vuông tại M có $\frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{M}^{2}}}\Rightarrow SO=\frac{\sqrt{3}}{6}$
Vậy \[SO=\frac{\sqrt{3}}{6};SA=\sqrt{S{{O}^{2}}+O{{A}^{2}}}=\frac{\sqrt{15}}{6}\xrightarrow{{}}R=\frac{5\sqrt{3}}{12}\]
Diện tích mặt cầu cần tính là $S=4\pi {{R}^{2}}=\frac{25\pi }{12}.$ Chọn A.
| Ví dụ 4: Cho ba tia $Sx,Sy,Sz$ không đồng phẳng và $\widehat{xSy}={{120}^{0}};\widehat{ySz}={{60}^{0}};\widehat{zSx}={{90}^{0}}.$ Trên các tia $Sx,Sy,Sz$ lấy lần lượt các điểm $A,B,C$ sao cho $SA=SB=SC=a.$ Tính bán kính $R$ của mặt cầu ngoại tiếp tứ diện A. $R=\frac{a}{2}.$ B. $R=a.$ C. $R=a\sqrt{2}.$ D. $R=a\sqrt{3}.$ |
Lời giải
Tam giác SAB có $Ab=\sqrt{S{{A}^{2}}+S{{B}^{2}}-2SA.SB.\cos \widehat{ASB}}=a\sqrt{3}$
Tam giác SAC vuông cân tại $S\xrightarrow{{}}AC=SA\sqrt{2}=a\sqrt{2}$
Suy ra $A{{C}^{2}}+B{{C}^{2}}=A{{B}^{2}}\xrightarrow{{}}\Delta ABC$ vuông tại C
Gọi O là trung điểm của $AB\xrightarrow{{}}SO\bot \left( ABC \right)$
Tam giác SAO vuông tại $O\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\frac{a}{2}$
Vậy $SO=\frac{a}{2};SA=a\xrightarrow{{}}R=\frac{S{{A}^{2}}}{2SO}=a.$ Chọn B.
| Ví dụ 5: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc ${{60}^{0}}.$ Thể tích của khối cầu ngoại tiếp khối chóp $S.ABCD$ là A. $\frac{4\pi {{a}^{3}}}{3}.$ B. $\frac{2\pi {{a}^{3}}\sqrt{6}}{9}.$ C. $\frac{8\pi {{a}^{3}}\sqrt{6}}{9}.$ D. $\frac{8\pi {{a}^{3}}\sqrt{6}}{27}.$ |
Lời giải
Gọi O là tâm hình vuông $ABCD\xrightarrow{{}}SO\bot \left( ABCD \right)$.
Do đó $\widehat{SB;\left( ABCD \right)}=\widehat{\left( SB;OB \right)}=\widehat{SBO}={{60}^{0}}.$
Tam giác SBO vuông tại O, có \[\left\{ \begin{matrix} SB=\frac{OB}{\cos \widehat{SBO}}\text{ } \\ SO=OB.\tan \widehat{SBO} \\\end{matrix} \right.\Rightarrow \left\{ \begin{matrix} SB=a\sqrt{2}\text{ } \\ SO=\frac{a\sqrt{6}}{2} \\\end{matrix} \right..\]
Suy ra bán kính mặt cầu cần tính là $R=\frac{S{{B}^{2}}}{2SO}={{\left( a\sqrt{2} \right)}^{2}}:\left( 2.\frac{a\sqrt{6}}{3} \right)=\frac{a\sqrt{6}}{3}.$
Vậy diện tích khối cầu cần tính là $V=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi .{{\left( \frac{a\sqrt{6}}{3} \right)}^{2}}=\frac{8\pi {{a}^{3}}\sqrt{6}}{27}.$ Chọn D.
| Ví dụ 6: Cho hình chóp $S.ABCD$ có $AC=2a,$ mặt bên $\left( SBC \right)$ tạo với mặt đáy $\left( ABCD \right)$ một góc ${{45}^{0}}.$ Bán kính mặt cầu ngoại tiếp hình chóp $S.ABCD$bằng A. \[\frac{\sqrt{2}}{4}a.\] B. \[\frac{a}{2}.\] C. \[\frac{3\sqrt{2}}{4}a.\] D. $\frac{a}{4}.$ |
Lời giải
Gọi M là trung điểm $BC\Rightarrow OM\bot BC\Rightarrow BC\bot \left( SMO \right)$.
Do đó $\widehat{\left( SBC \right);\left( ABCD \right)}=\widehat{\left( SM;MO \right)}=\widehat{SMO}={{45}^{0}}.$
Vì ABCD là hình vuông có $AC=2a\xrightarrow{{}}AB=a\sqrt{2}$
Tam giác SMO vuông cân tại $O\Rightarrow SO=OM=\frac{a\sqrt{2}}{2}$
Tam giác SAO vuông tại $O\Rightarrow SA=\sqrt{S{{O}^{2}}+O{{A}^{2}}}=\frac{a\sqrt{6}}{2}$
Vậy $SA=\frac{a\sqrt{6}}{2};SO=\frac{a\sqrt{2}}{2}\xrightarrow{{}}R=\frac{3\sqrt{2}}{4}a.$ Chọn C.
| Ví dụ 7: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SB và AD bằng $\sqrt{3}a.$ Bán kính mặt cầu ngoại tiếp hình chóp $S.ABCD$bằng A. $R=\frac{5\sqrt{6}}{12}a.$ B. $R=\frac{5\sqrt{3}}{3}a.$ C. $R=\frac{5\sqrt{3}}{12}a.$ D. $R=\frac{5\sqrt{6}}{3}a.$ |
Lời giải
Ta có $AD//BC\Rightarrow AD//\left( SBC \right)\Rightarrow d\left( SB;AD \right)=d\left( A;\left( SBC \right) \right)$
Gọi O là tâm hình vuông $ABCD\xrightarrow{{}}SO\bot \left( ABCD \right)$.
Gọi M là trung điểm $BC;$ kẻ $OH\bot SM\left( H\in SM \right)$
$\Rightarrow OH\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=2.OH\Rightarrow OH=\frac{a\sqrt{3}}{2}$
Tam giác SMO vuông, có $\frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{M}^{2}}}\Rightarrow SO=a\sqrt{3}$
Vậy $SO=a\sqrt{3};SA=\sqrt{S{{O}^{2}}+O{{A}^{2}}}=a\sqrt{5}\xrightarrow[{}]{}R=R=\frac{5\sqrt{6}}{3}a.$
Chọn D.
| Ví dụ 8: Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9, tính thể tích V của khối chóp có thể tích lớn nhất A. $V=144.$ B. $V=576.$ C. $V=576\sqrt{2}.$ D. $V=144\sqrt{6}.$ |
Lời giải
Xét mặt cầu $\left( S \right)$ ngoại tiếp hình chóp $S.ABCD$
Gọi O là tâm hình vuông $ABCD\xrightarrow{{}}SO\bot \left( ABCD \right)$
Bán kính mặt cầu $\left( S \right)$ là $R=\frac{S{{A}^{2}}}{2h}\Leftrightarrow S{{A}^{2}}=18h\text{ (*)}$
Đặt $AB=x\xrightarrow{{}}{{V}_{S.ABCD}}=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{h.{{x}^{2}}}{3}$
Tam giác SAO vuông tại $O\Rightarrow S{{A}^{2}}=S{{O}^{2}}+O{{A}^{2}}={{h}^{2}}+\frac{{{x}^{2}}}{2}$
Thay vào (*), ta được ${{h}^{2}}+\frac{{{x}^{2}}}{2}=18h\xrightarrow{{}}{{x}^{2}}=36h-2{{h}^{2}}$
Do đó $V=\frac{h}{3}.\left( 36h-2{{h}^{2}} \right)=12{{h}^{2}}-\frac{2}{3}{{h}^{3}}\xrightarrow{casio}{{V}_{\max }}=576.$ Chọn B.
Lý thuyết Toán Lớp 12