Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy – bài tập có đáp án chi tiết

Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy – bài tập có đáp án
Phương pháp giải bài toán chứng minh 3 điểm thẳng hàng, đồng quy.
Để chứng minh ba điểm (hay nhiều điểm) thẳng hàng ta chứng minh chúng là điểm chung của hai mặt phẳng phân biệt, khi đó chúng nằm trên đường thẳng giao tuyến của hai mặt phẳng nên thẳng hàng.
Để chứng minh ba đường thẳng đồng quy ta chứng minh giao điểm của hai đường thẳng thuộc đường thẳng còn lại
Bài tập trắc nghiệm chứng minh 3 điểm thẳng hàng hoặc đồng quy có Lời giải chi tiết
| Bài tập 1: Cho tứ diện S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh I, J, K thẳng hàng. |
Lời giải chi tiết
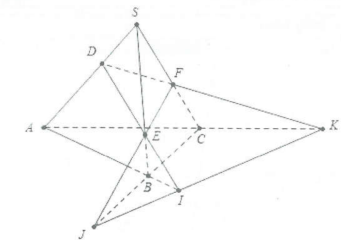
Ta có: $I=DE\cap AB\Rightarrow \left\{ \begin{array} {} I\in \left( \text{DEF} \right) \\ {} I\in \left( ABC \right) \\ \end{array} \right.\Rightarrow I\in $ giao tuyến của hai mặt phẳng (DEF) và (ABC).
Tương tự $J=\text{EF}\cap BC\Rightarrow J$ thuộc giao tuyến của hai mặt phẳng (DEF) và (ABC).
$K=FD\cap AC\Rightarrow K$ thuộc giao tuyến của hai mặt phẳng (DEF) và (ABC).
Do đó I, J, K thẳng hàng do cùng thuộc đường thẳng giao tuyến của hai mặt phẳng (DEF) và (ABC).
| Bài tập 2: Cho hình bình hành ABCD, S là điểm không thuộc mp(ABCD), M và N lần lượt là trung điểm của đoạn AB và SC. a) Xác định giao điểm $I=AN\cap \left( SBD \right)$ . b) Xác định giao điểm $J=MN\cap \left( SBD \right)$ . c) Chứng minh I, J, B thẳng hàng. |
Lời giải chi tiết
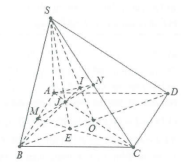
a) Gọi $O=AC\cap BD$ và $I=AN\cap SO$
Khi đó $I\in SO\Rightarrow I\in \left( SBD \right)\Rightarrow I=AN\cap \left( SBD \right)$
b) Gọi $E=CM\cap BD$
Trong mặt phẳng (SCM) gọi $J=MN\cap SE$
Khi đó $J=MN\cap \left( SBD \right)$.
c) Các điểm I, J, B lần lượt thuộc các đường thẳng AI, MN, AM nên I, J, B $\in mp\left( AMN \right)$
Mặt khác các điểm I, J, B $\in \left( SBD \right)$.
Do đó I, J, B thuộc giao tuyến của 2 mặt phẳng (AMN) và (SBD) $\Rightarrow I,J,B$ thẳng hàng.
| Bài tập 3: Cho tứ diện SABC. Gọi L, M, N lần lượt là các điểm trên các cạnh SA, SB và AC sao cho LM không song song với AB, LN không song song với SC. a) Tìm giao tuyến của mp(LMN) và (ABC) b) Tìm giao điểm $I=BC\cap \left( LMN \right)$ và $J=SC\cap \left( LMN \right)$ . c) Chứng minh M, I, J thẳng hàng. |
Lời giải chi tiết
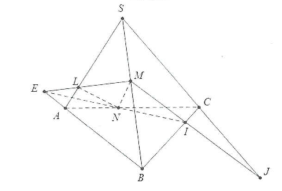
a) Trong mặt phẳng (SAB) gọi $E=LM\cap AB,$ khi đó 2 mặt phẳng (LMN) và (ABC) có 2 điểm chung là E và N suy ra $\left( LMN \right)\cap \left( ABC \right)=EN$
b) Trong mặt phẳng (ABC) gọi $I=BC\cap EN$ khi đó $I=BC\cap \left( LMN \right)$
Trong mặt phẳng (SAC) gọi $J=LN\cap SC$ khi đó $J=SC\cap \left( LMN \right)$ .
c) 3 điểm M, I, J cùng thuộc 2 mặt phẳng (LMN) và (SBC) $\Rightarrow $ M, I, J thuộc giao tuyến của 2 mặt phẳng (LMN) và (SBC) $\Rightarrow $ M, I, J thẳng hàng.
| Bài tập 4: Cho tứ giác ABCD và điểm SÏ(ABCD). Gọi M, N là hai điểm trên BC và SD. a) Tìm giao điểm $I=BN\cap \left( SAC \right)$ b) Tìm giao điểm $I=MN\cap \left( SAC \right).$ c) Chứng minh C, I, J thẳng hàng. |
Lời giải chi tiết
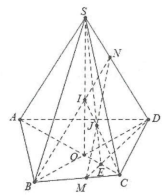
a) Nối $AC\cap BD=O;$ Nối $SO\cap BN=1.$
Suy ra I là giao điểm của BN và (SAC).
b) Nối MD cắt AC tại E.
Nối SE cắt MN tại J $\Rightarrow $ J là giao điểm của MN và (SAC).
c) Ta có $I=BN\cap SO\Rightarrow IC=\left( SAC \right)\cap \left( BCN \right).$
Và $J=MN\cap SE\Rightarrow JC=\left( SAC \right)\cap \left( BCN \right).$
Do đó, ba điểm C, I, J thẳng hàng $\Rightarrow $ Đpcm.
| Bài tập 5: Cho tứ giác ABCD và SÏ(ABCD). Gọi I, J là hai điểm trên AD và SB, AD cắt BC tại O và OJ cắt SC tại M. a) Tìm giao điểm K = IJ và (SAC). b) Xác định giao điểm L = DJ và (SAC). c) Chứng minh A, K, L, M thẳng hàng. |
Lời giải chi tiết
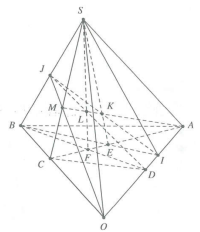
a) Trong mp(ABCD), gọi $E=AC\cap BI$
Trong mặt phẳng (SBI) gọi $K=\text{IJ}\cap SE$
Khi đó $K=\text{IJ}\cap \left( SAC \right)$
b) Gọi $F=AC\cap BD$
Trong mặt phẳng (SBD) gọi $L=DJ\cap SF$
Khi đó $L=DJ\cap \left( SAC \right)$
c) Các điểm K, L, A, M đều thuộc mặt phẳng (SAC) và (OAJ) do đó chúng thuộc giao tuyến của 2 mặt phẳng (SAC) và (OAJ) suy ra A, K, L, M thẳng hàng.
Cách Tìm nhanh thiết diện của hình chóp và mặt phẳng (P) – Bài tập có đáp án
Phương pháp tìm thiết diện giữa hình chóp và mặt phẳng
Thiết diện của hình chóp và mặt phẳng (P) là đa giác giới hạn bởi các đoạn giao tuyến của (P) với các mặt của hình chóp (nối các giao điểm của (P) với các cạnh của hình chóp).
Bài tập trắc nghiệm xác định thiết diện của hình chóp và mặt phẳng có Lời giải chi tiết
| Bài tập 1: Cho hình chóp tứ giác S.ABCD. Ba điểm A’, B’, C’ lần lượt nằm trên ba cạnh SA, SB,SC nhưng không trùng với S, A, B, C. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (A’, B’, C’). |
Lời giải chi tiết
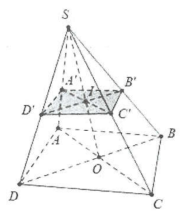
Trong mặt phẳng (ABC) gọi $O=AC\cap BD$
Trong mặt phẳng (SAC) gọi $I=SO\cap A'C'\Rightarrow I\in \left( SBD \right)\cap \left( A'B'C' \right).$
Trong mp(SBD) gọi $D'=BI\cap SD\Rightarrow $ thiết diện của hình chóp khi cắt bởi mặt phẳng (A’B’C’) là tứ giác A’B’C’D’.
| Bài tập 2: Cho hình chóp S.ABCD, M là một điểm trên cạnh SC, N và P lần lượt là trung điểm của AB và AD. Tìm thiết diện của hình chóp với mặt phẳng (MNP) |
Lời giải chi tiết
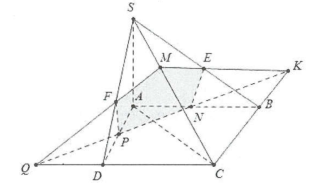
Trong mặt phẳng (ABCD) gọi $Q=NP\cap CD$ và $K=NP\cap BC$
Trong mp(SBC) gọi $E=SB\cap KM,$ trong mp(SAD) gọi $F=SD\cap QM.$
Thiết diện của hình chóp với mặt phẳng (MNP) là ngũ giác NEMFP.
| Bài tập 3: Cho tứ diện đều ABCD, cạnh bằng a. Kéo dài BC một đoạn CE = a. Kéo dài BD một đoạn DF = a. Gọi M là trung điểm của AB. a) Tìm thiết diện của tứ diện với mặt phẳng (MEF). b) Tính diện tích của thiết diện. |
Lời giải chi tiết
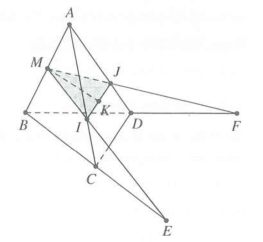
a) Trong mp(ABC): Dựng ME cắt AC tại I.
Trong mp(ABD): Dựng MF cắt AD tại J.
Từ đó thiết diện của tứ diện với mp(MEF) là $\Delta M\text{IJ}.$
b) Theo cách dựng thì I và J lần lượt là trọng tâm tam giác ABE và ABF.
$\Rightarrow \left\{ \begin{array} {} AI=\frac{2}{3}AC=\frac{2a}{3} \\ {} \text{AJ=}\frac{2}{3}AD=\frac{2a}{3} \\ \end{array} \right.\Rightarrow $ tam giác AIJ đều $\Rightarrow \text{IJ}=\frac{2a}{3}.$
Mặt khác $AI=AJ$ nên $\Delta AMI=\Delta \text{AMJ}\Rightarrow MI=MJ.$
Trong $\Delta AMI,MI=\sqrt{M{{A}^{2}}+I{{A}^{2}}-2MA.IA.\cos A}=\frac{a\sqrt{13}}{6}$
${{S}_{\Delta MJI}}=\frac{1}{2}\text{IJ}.MK=\frac{1}{2}.\frac{2a}{3}.2\sqrt{{{\left( \frac{a\sqrt{13}}{6} \right)}^{2}}-{{\left( \frac{a}{3} \right)}^{2}}}=\frac{{{a}^{2}}}{6}$
| Bài tập 4: Cho hình chóp S.ABCD, M là một điểm trên cạnh BC, N là một điểm trên cạnh SD. a) Tìm giao điểm I của BN và (SAC) và giao điểm J của MN và (SAC). b) DM cắt AC tại K. Chứng minh S, K, J thẳng hàng. c) Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (BCN). |
Lời giải chi tiết
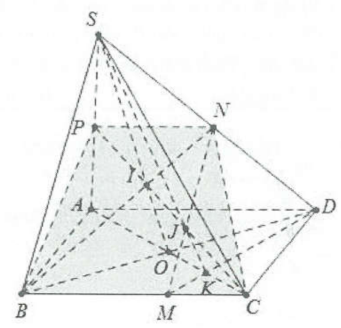
a) Gọi O là giao điểm AC và BD.
Trong mp(SBD), BN cắt SO tại đâu đó chính là điểm I.
Trong mp(ABCD), DM giao AC tại E.
Trong mp(SDM), $SE\cap MN=J$ .
b) Dễ thấy 3 điểm S, K, J đều thuộc 2 mặt phẳng là (SAC) và (SDM) nên 3 điểm S, K, J thuộc giao tuyến của 2 mặt phẳng trên hay chúng thẳng hàng.
c) Trong mp(SAC), kẻ CI giao SA tại O.
Từ đó thiết diện tạo bởi mp(BNC) với hình chóp từ tứ giác BCNP.
| Bài tập 5: Cho hình chóp SABCD có đáy là hình bình hành. Điểm M là trung điểm của SB và G là trọng tâm của tam giác SAD. a) Tìm giao điểm I của MG với (ABCD), chứng tỏ điểm D thuộc mặt phẳng (CMG). b) Chứng tỏ (CMG) đi qua trung điểm của SA, tìm thiết diện của hình chóp với (CMG). c) Tìm thiết diện của hình chóp với (AMG). |
Lời giải chi tiết
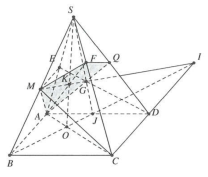
a) Trong mặt phẳng (SAD), gọi $J=SG\cap AD$ .
Trong mp(SBJ), gọi $I=MG\cap BJ\Rightarrow I=MG\cap \left( ABC \right)\Rightarrow I\in \left( CMG \right)$
Ta có: J là trung điểm của AD $\Rightarrow JD=\frac{1}{2}BC$ mà
$JD\parallel BC\Rightarrow JD$ là đường trung bình trong
$\Delta IBC\Rightarrow D$ là trung điểm của CI hay $D\in \left( CMJ \right)$
Do đó $D\in \left( CMG \right)$
b) Ta có $\left( CMG \right)\equiv \left( CIM \right)$
Trong mp(SAD), dựng DG cắt SA tại E. Mặt khác, do G là trọng tâm $\Delta SAD\Rightarrow E$ là trung điểm của SA.
Như vậy tứ giác CMED là thiết diện của (CMG) với khối chóp
c) Gọi $O=BJ\cap AC,$
Trong mp(SBI), gọi $K=SO\cap MI.$ Trong mp(SAD), dựng AG cắt SD tại Q.
Trong mp(SAC), dựng AK cắt SC tại F, như vậy tứ giác AMFQ là thiết diện của khối chóp với mặt phẳng (AMG).
| Bài tập 6: Cho hình chóp tứ giác S.ABCD, có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD, P không trùng với S và D. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Thiết diện của hình chóp cắt bởi (MNP) là hình gì? A. Tam giác. B. Tứ giác. C. Ngũ giác. D. Lục giác. |
Lời giải chi tiết
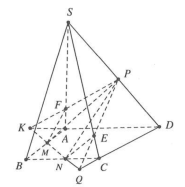
Gọi $\left\{ \begin{array} {} K=AD\cap MN;Q=CD\cap MN \\ {} F=PK\cap SA;E=PQ\cap SC \\ \end{array} \right.$
Thiết diện là ngũ giác MNEPF. Chọn C.
| Bài tập 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P là ba điểm trên các cạnh AD, CD, SO sao cho M, N, P không trùng với các đỉnh. Thiết diện của hình chóp với mặt phẳng (MNP) là hình gì? A. Tứ giác. B. Ngũ giác. C. Tam giác. D. Lục giác. |
Lời giải chi tiết
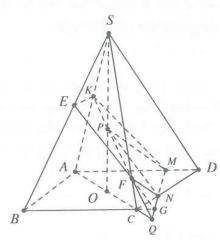
Gọi $\left\{ \begin{array} {} Q=AC\cap MN;K=SA\cap PQ;F=SC\cap PQ \\ {} G=BC\cap M;E=SB\cap GF \\ \end{array} \right.$
Thiết diện là ngũ giác MNFEK. Chọn B
Lý thuyết Toán Lớp 12