Cách tính Khoảng cách từ chân đường cao đến mặt phẳng bên.

Cách tính Khoảng cách từ chân đường cao đến mặt phẳng bên.
Xét bài toán khoảng cách trong không gian.
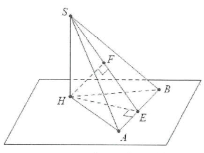
Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ điểm H đến mặt bên $\left( SAB \right)$.
Dựng $HE\bot AB,\left( E\in AB \right)$ ta có:
$\left\{ \begin{array} {} AB\bot SH \\ {} AB\bot HE \\ \end{array} \right.\Rightarrow AB\bot \left( SHE \right)$$\left( 1 \right)$.
Dựng $HF\bot SE,\left( F\in SE \right)$. Từ $\left( 1 \right)$ $HF\bot AB$
Do đó $HF\bot \left( SAB \right)\Rightarrow d\left( H;\left( SAB \right) \right)=HF$.
Cách tính: Xét tam giác SHE vuông tại H có đường cao HF ta có: $\frac{1}{H{{F}^{2}}}=\frac{1}{H{{E}^{2}}}+\frac{1}{S{{H}^{2}}}$
Hay $HF=\frac{HE.SH}{\sqrt{H{{E}^{2}}+S{{H}^{2}}}}$.
Bài tập khoảng cách từ chân đường cao đến mặt phẳng bên có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có $AB=a,BC=a\sqrt{3}$. Biết $SA=2a$ và $SA\bot \left( ABC \right)$. a) Tính khoảng cách từ A đến mặt phẳng $\left( SBC \right)$. b) Gọi M là trung điểm của AC. Tính khoảng cách từ A đến mặt phẳng $\left( SBM \right)$. |
Lời giải chi tiết
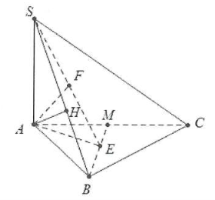
a) Ta có : $AB\bot BC$, mặt khác $BC\bot SA\Rightarrow BC\bot \left( SAB \right)$.
Dựng $AH\bot SB\Rightarrow $ $\left\{ \begin{array} {} AH\bot SB \\ {} AH\bot BC \\ \end{array} \right.\Rightarrow AH\bot \left( SBC \right)$.
Khi đó $d\left( A;\left( SBC \right) \right)=AH=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{2a}{\sqrt{5}}$.
b) Dựng $AE\bot BM,AF\bot SE$ ta có:
$\left\{ \begin{array} {} AE\bot BM \\ {} AE\bot BM \\ \end{array} \right.\Rightarrow BM\bot \left( SAE \right)\Rightarrow BM\bot \text{AF}$.
Khi đó: $\left\{ \begin{array} {} AF\bot SE \\ {} AF\bot BM \\ \end{array} \right.\Rightarrow AF\bot \left( SBM \right)$.
Ta có: $AB=a,AC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=2a$. Do BM là đường trung tuyến ứng với cạnh huyền nên
$BM=\frac{1}{2}AC=AM=AB=a\Rightarrow \Delta ABM$ đều cạnh $a$$\Rightarrow AE=\frac{a\sqrt{3}}{2}$.
Khi đó $d\left( A;\left( SBM \right) \right)=\frac{AE.SA}{\sqrt{A{{E}^{2}}+S{{A}^{2}}}}=\frac{2a\sqrt{57}}{19}$.
| Bài tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh $2a$, $SA\bot \left( ABC \right)$. Đường thẳng SB tạo với đáy một góc $60{}^\circ $. a) Tính khoảng cách từ A đến mặt phẳng $\left( SBC \right)$. b) Tính khoảng cách từ A đến mặt phẳng $\left( SCM \right)$, với M là trung điểm của cạnh AB. |
Lời giải chi tiết
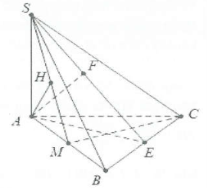
a) Do $SA\bot \left( ABC \right)\Rightarrow \widehat{\left( SB;\left( ABC \right) \right)}=\widehat{SBA}=60{}^\circ $.
Do đó $SA=AB\tan 60{}^\circ =2a\sqrt{3}$.
Dựng $AE\bot BC,\Delta ABC$ đều nên $\frac{AB\sqrt{3}}{2}=a\sqrt{3}$.
Dựng $AF\bot SE$, mặt khác $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AE \\ \end{array} \right.\Rightarrow BC\bot \text{AF}$.
$\Rightarrow AF\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AF=\frac{SA.AE}{\sqrt{S{{A}^{2}}+A{{E}^{2}}}}=\frac{2a\sqrt{21}}{7}$.
b) Do M là trung điểm của AB nên $CM\bot AB$.
Mặt khác $CM\bot SA\Rightarrow CM\bot \left( SAM \right)$. Dựng $AH\bot SM\Rightarrow AH\bot \left( SMC \right)$.
Khi đó $d\left( A;\left( SMC \right) \right)=\frac{SA.AM}{\sqrt{S{{A}^{2}}+A{{M}^{2}}}}=\frac{2a}{\sqrt{5}}$.
| Bài tập 3: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết $OA=a,OB=b,OC=c$. Tính khoảng cách d từ O đến mặt phẳng $\left( ABC \right)$. |
Lời giải chi tiết
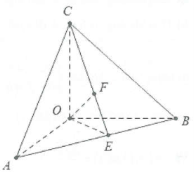
Do $\left\{ \begin{array} {} OC\bot OA \\ {} OC\bot OB \\ \end{array} \right.\Rightarrow OC\bot \left( OAB \right)\Rightarrow AB\bot OC$.
Dựng $OE\bot AB,OF\bot CE$ suy ra $\text{OF}\bot BC$.
Khi đó $OF\bot \left( ABC \right)\Rightarrow d\left( O;\left( ABC \right) \right)=OF$.
Mặt khác: $\frac{1}{O{{F}^{2}}}=\frac{1}{O{{C}^{2}}}+\frac{1}{O{{E}^{2}}}$ và $\frac{1}{O{{E}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}$
Do đó $\frac{1}{{{d}^{2}}\left( O;\left( ABC \right) \right)}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}$
Vậy $d=\frac{abc}{\sqrt{{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}}}$.
| Bài tập 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SB vuông góc với mặt phẳng đáy. Cho biết $SB=3a,AB=4a,BC=2a$. Tính khoảng cách từ B đến mặt phẳng $\left( SAC \right)$. A. $\frac{12a\sqrt{61}}{61}$ B. $\frac{4a}{5}$ C. $\frac{12a\sqrt{29}}{29}$ D. $\frac{3a\sqrt{14}}{14}$ |
Lời giải chi tiết
Ta có: BS, BA, BC đôi một vuông góc với nhau nên ta có:
$\frac{1}{{{d}^{2}}\left( B;\left( SAC \right) \right)}=\frac{1}{S{{B}^{2}}}+\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}=\frac{1}{9{{a}^{2}}}+\frac{1}{16{{a}^{2}}}+\frac{1}{4{{a}^{2}}}=\frac{61}{144{{a}^{2}}}$
Do đó $d\left( B;\left( SAC \right) \right)=\frac{12a\sqrt{61}}{61}$. Chọn A.
| Bài tập 5: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B và $AB=a,BC=a\sqrt{3}$. Hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của cạnh AC. Biết $SH=a$, tính khoảng cách từ H đến các mặt phẳng $\left( SAB \right)$ và $\left( SAC \right)$. |
Lời giải chi tiết
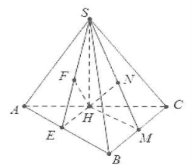
Dựng $HE\bot AB$ và $HF\bot SE$ thì ta có $d\left( H;\left( SAB \right) \right)=HF$.
Mặt khác HE là đường trung bình trong tam giác ABC nên $HE=\frac{BC}{2}=\frac{a\sqrt{3}}{2}$.
Khi đó $d\left( H;\left( SAB \right) \right)=HF=\frac{HE.SH}{\sqrt{H{{E}^{2}}+S{{H}^{2}}}}=\frac{a\sqrt{21}}{7}$.
Tương tự dựng $HM\bot BC,HN\bot SM\Rightarrow d\left( H;\left( SBC \right) \right)=HN$
Mặt khác $HM=\frac{AB}{2}=\frac{a}{2}\Rightarrow HN=\frac{SH.HM}{\sqrt{S{{H}^{2}}+H{{M}^{2}}}}=\frac{a}{\sqrt{5}}$.
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có $AB=a,AD=2a$, SA vuông góc với đáy và $SA=a$. a) Tính khoảng cách từ A đến mặt phẳng $\left( SCD \right)$ và $\left( SBC \right)$. b) Tính khoảng cách từ A đến mặt phẳng $\left( SBD \right)$. |
Lời giải chi tiết
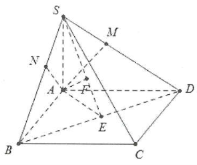
a) Dựng $AN\bot SB$. Do $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AB \\ \end{array} \right.\Rightarrow BC\bot AN$.
$AN\bot \left( SBC \right)\Rightarrow d\left( A;\left( SBC \right) \right)=AN=\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}$
Vậy $\left( A;\left( SBC \right) \right)=\frac{a\sqrt{2}}{2}$.
Tương tự $d\left( A;\left( SCD \right) \right)=AM=\frac{SA.AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}=\frac{2a}{\sqrt{5}}$.
b) Dựng $AE\bot BD,\text{AF}\bot SE$.
Ta chứng minh được $d\left( A;\left( SBD \right) \right)=d=AF$
Vì $AS\bot AB\bot AD\Rightarrow \frac{1}{{{d}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{D}^{2}}}+\frac{1}{S{{A}^{2}}}\Rightarrow d=\frac{2a}{3}$.
| Bài tập 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh $2a$. Hình chiếu vuông góc của đỉnh S lên mặt đáy trùng với trung điểm H của AB. Biết $SD=3a$. a) Tính khoảng cách từ H đến mặt phẳng $\left( SCD \right)$. b) Tính khoảng cách từ điểm H đến mặt phẳng $\left( SBD \right)$. |
Lời giải chi tiết
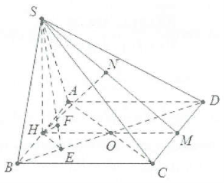
a) Ta có: $HD=\sqrt{A{{H}^{2}}+A{{D}^{2}}}=a\sqrt{5}$
Mặt khác $SH=\sqrt{S{{D}^{2}}-D{{H}^{2}}}=2a$.
Dựng $HM\bot CD,HN\bot SM\Rightarrow d\left( H;\left( SCD \right) \right)=HN$.
Do AHMD là hình chữ nhật nên $AD=HM=2a$.
Khi đó $d\left( H;\left( SCD \right) \right)=\frac{SH.HM}{\sqrt{S{{H}^{2}}+H{{M}^{2}}}}=a\sqrt{2}$.
b) Dựng $HE\bot BD;HF\bot SE$ khi đó $d\left( H;\left( SBD \right) \right)=HF$
Ta có: $AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow HE=\frac{OA}{2}=\frac{a\sqrt{2}}{2}$
Do đó $\frac{1}{H{{F}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{E}^{2}}}\Rightarrow HF=\frac{2a}{3}\Rightarrow d\left( H;\left( SBD \right) \right)=HF=\frac{2a}{3}$.
| Bài tập 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi có tam giác ABC đều cạnh $a$. Gọi H là trung điểm của AB. Biết SH vuông góc với mặt đáy, mặt phẳng $\left( SCD \right)$ tạo với đáy một góc $60{}^\circ $. Tính a) Khoảng cách từ H đến mặt phẳng $\left( SCD \right)$. b) Khoảng cách từ H đến mặt phẳng $\left( SBC \right)$. |
Lời giải chi tiết
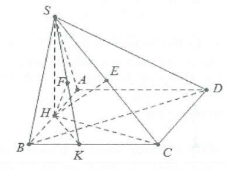
a) Do $\Delta ABC$ đều nên $CH\bot AB\Rightarrow CH\bot CD$
$CH\bot \left( SHC \right)\Rightarrow \widehat{SCH}=60{}^\circ ,CH=\frac{a\sqrt{3}}{2}$.
Ta có: $SH=CH\tan 60{}^\circ =\frac{3a}{2}$.
$HK\bot BC,HK=\frac{a\sqrt{3}}{4};HF\bot SK\Rightarrow HF\bot \left( SBC \right)$
Mặt khác: $HF=\frac{HK.SH}{\sqrt{H{{K}^{2}}+S{{H}^{2}}}}=\frac{\sqrt{42}a}{14}$.
Khi đó $d\left( H;\left( SBC \right) \right)=\frac{a\sqrt{42}}{14}$
b) Dựng $HE\bot SC$ ta có: $HE\bot \left( SCD \right)$.
Ta có: $HE=\frac{HC.SH}{\sqrt{H{{C}^{2}}+S{{H}^{2}}}}=\frac{3a}{4}\Rightarrow d\left( H;\left( SCD \right) \right)=HE=\frac{3a}{4}$.
| Bài tập 9: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có $AB=BC=\frac{AD}{2}$. Mặt phẳng $\left( SAB \right)$ và $\left( SAD \right)$ cùng vuông góc với mặt đáy. Biết $SA=2a$ và đường thẳng SD tạo với mặt phẳng $\left( SAC \right)$ một góc $30{}^\circ $. tính a) Khoảng cách từ A đến mặt phẳng $\left( SCD \right)$. b) Khoảng cách từ A đến mặt phẳng $\left( SBC \right)$. |
Lời giải chi tiết
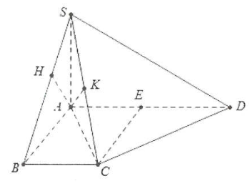
a) Do $\left\{ \begin{array} {} \left( SAB \right)\bot \left( ABCD \right) \\ {} \left( SAD \right)\bot \left( ABCD \right) \\ \end{array} \right.\Rightarrow SA\bot \left( ABCD \right)$.
Đặt $AB=BC=\frac{AD}{2}=x$, gọi E là trung điểm của AC ta có: $CE=AB=\frac{1}{2}AD$ $\Rightarrow \Delta ACD$ vuông tại C (tính chất trung tuyến ứng cạnh huyền trong tam giác vuông).
+) Khi đó ta có: $SC=\sqrt{2{{x}^{2}}+4{{a}^{2}}},CD=x\sqrt{2}$.
+) Mặt khác: $\left\{ \begin{array} {} CD\bot SA \\ {} CD\bot AC \\ \end{array} \right.\Rightarrow CD\bot \left( SAC \right)$.
Do đó $\widehat{\left( SD;\left( SAC \right) \right)}=\widehat{DSC}=30{}^\circ \Rightarrow \tan 30{}^\circ =\frac{DC}{SC}\Rightarrow \frac{x\sqrt{2}}{\sqrt{2{{x}^{2}}+4{{a}^{2}}}}=\frac{1}{\sqrt{3}}\Leftrightarrow 4{{x}^{2}}=4{{a}^{2}}\Leftrightarrow x=a$.
Dựng $AK\bot SC\Rightarrow AK\bot \left( SCD \right)\Rightarrow d\left( A;\left( SCD \right) \right)=AK=\frac{SA.AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{2a}{\sqrt{3}}$.
b) Dựng $AH\bot SB$, ta có: $\left\{ \begin{array} {} BC\bot SA \\ {} BC\bot AB \\ \end{array} \right.\Rightarrow BC\bot AH$.
Mặt khác: $AH\bot SB\Rightarrow AH\bot \left( SBC \right)$.
Do đó $AH=\frac{AB.SA}{\sqrt{A{{B}^{2}}+S{{A}^{2}}}}=\frac{2a}{\sqrt{5}}\Rightarrow d\left( A;\left( SBC \right) \right)=AH=\frac{2a}{\sqrt{5}}$.
| Bài tập 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAD là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết $SA=a\sqrt{2}$ và SB tạo với đáy một góc $30{}^\circ $. Gọi H là trung điểm của AD. Tính các khoảng cách sau: a) $d\left( H;\left( SBC \right) \right)$ b) $d\left( H;\left( SAC \right) \right)$ |
Lời giải chi tiết
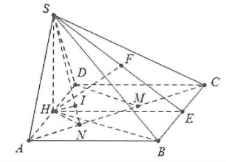
a) Gọi H là trung điểm của AD ta có: $SH\bot AD$
Lại có: $\left( SAD \right)\bot \left( ABCD \right)\Rightarrow SH\bot \left( ABCD \right)$.
Mặt khác: $AD=SA\sqrt{2}=2a\Rightarrow SH=\frac{1}{2}AD=a$.
$\widehat{SBH}=30{}^\circ \Rightarrow HB\tan 30{}^\circ =SH=a\Rightarrow HB=a\sqrt{3}$
Khi đó: $AB=\sqrt{H{{B}^{2}}-A{{H}^{2}}}=a\sqrt{2}$
Dựng $\left\{ \begin{array} {} HE\bot BC \\ {} HE\bot SE \\ \end{array} \right.$ ta có: $BC\bot HF$ từ đó suy ra $HF\bot \left( SBC \right)\Rightarrow d\left( H;\left( SBC \right) \right)=HF$.
Ta có: $\frac{1}{H{{F}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{E}^{2}}}\Rightarrow HF=\frac{a\sqrt{6}}{3}=d\left( H;\left( SBC \right) \right)$.
b) Dựng $HN\bot AC\Rightarrow AC\bot \left( SHN \right)$, dựng $HI\bot SN\Rightarrow HI\bot \left( SAC \right)$
Dựng $DM\bot AC\Rightarrow DM=\frac{2a\sqrt{2}}{\sqrt{6}}\Rightarrow HN=\frac{a}{\sqrt{3}}\Rightarrow HI=\frac{HN.SH}{\sqrt{H{{N}^{2}}+S{{H}^{2}}}}=\frac{a}{2}$.
Do đó $d\left( H;\left( SAC \right) \right)=HI=\frac{a}{2}$
| Bài tập 11: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân $\left( AD//BC \right)$ có $AB=BC=CD=a,AD=2a$, SA vuông góc với đáy. Biết mặt phẳng $\left( SCD \right)$ tạo với mặt phẳng $\left( ABCD \right)$ một góc $60{}^\circ $. Tính cách các khoảng cách sau: a) $d\left( A;\left( SCD \right) \right)$ b) $d\left( A;\left( SBC \right) \right)$ |
Lời giải chi tiết
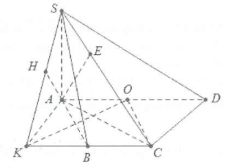
a) Gọi O là trung điểm của cạnh AD ta có tứ giác ABCO là hình bình hành $\Rightarrow AB=CO=a=\frac{1}{2}AD$ do đó $\widehat{ACD}=90{}^\circ \Rightarrow AC\bot CD$ mà $SA\bot CD$ nên $\left( SAC \right)\bot CD\Rightarrow \widehat{SCA}=60{}^\circ $.
+) Ta có: $AC=\sqrt{A{{D}^{2}}-C{{D}^{2}}}=a\sqrt{3}$ suy ra $SA=AC\tan 60{}^\circ =3a$
+) Dựng $AE\bot SC,AE\bot CD\Rightarrow AE\bot \left( SCD \right)$.
+) Khi đó $d\left( B;SCD \right)=d\left( O;SCD \right)=\frac{1}{2}d\left( A;\left( SCD \right) \right)$.
+) Ta có: $AE=\frac{SA.AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{3a}{2}\Rightarrow d\left( A;\left( SCD \right) \right)=AE=\frac{3a}{2}$.
b) Dựng $AK\bot BC,AH\bot SK\Rightarrow AH\bot \left( SBC \right)$
+) Ta có: $d\left( A;\left( SBC \right) \right)=AH$.
+) Mặt khác: $AK=d\left( C;AD \right)=\frac{AC.CD}{\sqrt{A{{C}^{2}}+C{{D}^{2}}}}=\frac{a\sqrt{3}}{2}\Rightarrow AH=\frac{AK.SA}{\sqrt{S{{A}^{2}}+A{{K}^{2}}}}=\frac{3a}{\sqrt{13}}$
Do đó $d\left( A;\left( SBC \right) \right)=AH=\frac{3a}{\sqrt{13}}$.
| Bài tập 12: Cho hình lăng trụ đứng $ABC.A'B'C'$có đáy là tam giác đều cạnh $a$, gọi I là trung điểm cạnh BC, đường thẳng A’C tạo với đáy một góc $60{}^\circ $. a) Tính khoảng cách từ A đến mặt phẳng $\left( A'BC \right)$. b) Tính khoảng cách từ A đến mặt phẳng $\left( \alpha \right)$ chứa A’I và song song với AC. |
Lời giải chi tiết
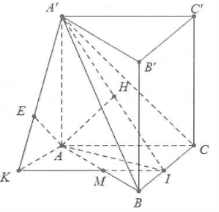
a) Do $AA'\bot \left( ABC \right)\Rightarrow \widehat{\left( A'C;\left( ABC \right) \right)}=\widehat{A'CA}$.
Ta có: $\widehat{A'CA}=60{}^\circ \Rightarrow AA'=AC\tan 60{}^\circ =a\sqrt{3}$
Dựng $AI\bot BC\Rightarrow BC\bot \left( A'AI \right)$ và $AI=\frac{a\sqrt{3}}{2}$
Dựng $AH\bot A'I\Rightarrow d\left( A;\left( A'BC \right) \right)=AH$
Ta có: $AH=\frac{AI.AA'}{\sqrt{A{{I}^{2}}+AA{{'}^{2}}}}=\frac{a\sqrt{15}}{5}$
Vậy $d\left( A;\left( A'BC \right) \right)=AH=\frac{a\sqrt{15}}{5}$
b) Dựng $Ix//AC\Rightarrow \left( \alpha \right)\equiv \left( A'Ix \right)$
Khi đó: $d\left( A;\left( \alpha \right) \right)=d\left( A;\left( A'Ix \right) \right)$, Ix cắt AB tại trung điểm M và AB.
Dựng $AK\bot Ix,AE\bot A'K$
Do $IM//AC\Rightarrow \widehat{AMK}=\widehat{MAC}=60{}^\circ $ suy ra $AK=AM\sin \widehat{AMK}=\frac{a}{2}\sin 60{}^\circ =\frac{a\sqrt{3}}{4}$
Ta có: $d\left( A;\left( A'IK \right) \right)=AE=\frac{AK.A'A}{\sqrt{A{{K}^{2}}+A'{{A}^{2}}}}=\frac{a\sqrt{51}}{17}$
| Bài tập 13: Cho hình lăng trụ $ABC.A'B'C'$có đáy là tam giác vuông cân tại A với $AB=AC=3a$. Hình chiếu vuông góc của B’ lên mặt đáy là điểm H thuộc BC sao cho $HC=2HB$. Biết cạnh bên của lăng trụ bằng $2a$. a) Tính khoảng cách từ H đến mặt phẳng $\left( B'AC \right)$. b) Tính khoảng cách từ H đến mặt phẳng $\left( BAA'B' \right)$. |
Lời giải chi tiết
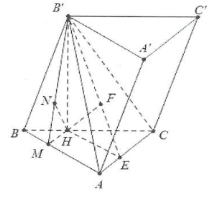
a) Ta có: BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=3a\sqrt{2}\Rightarrow HB=a\sqrt{2}$
Lại có $B'H=\sqrt{BB{{'}^{2}}-H{{B}^{2}}}=a\sqrt{2}$
Dựng $HE\bot AC,HF\bot B'E\Rightarrow HF\bot \left( B'AC \right)$
Áp dụng định lý Talet trong tam giác BAC ta có:
$\frac{HE}{AB}=\frac{CH}{BC}=\frac{2}{3}\Rightarrow HE=2a\Rightarrow HF=\frac{HE.B'H}{\sqrt{H{{E}^{2}}+B'{{H}^{2}}}}=\frac{2a}{\sqrt{3}}$
Do có: $d\left( H;\left( B'AC \right) \right)=HF=\frac{2a}{\sqrt{3}}$
b) Dựng $HM\bot AB,HN\bot B'M$
Khi đó $d\left( H;\left( B'BA \right) \right)=HN$.
Ta có: $HM=\frac{AC}{3}=a\Rightarrow HN=\frac{HB'.HM}{\sqrt{HB{{'}^{2}}+H{{M}^{2}}}}=\frac{a\sqrt{6}}{3}$.
Lý thuyết Toán Lớp 12