Giải phương trình mũ - Sử dụng tính đơn điệu của hàm số, phương pháp phân tích nhân tử, phương pháp đánh giá

Giải phương trình mũ - Sử dụng tính đơn điệu của hàm số, phương pháp phân tích nhân tử, phương pháp đánh giá

Để giải các bài toán bằng các phương pháp này ta cần ghi nhớ một số kiến thức sau:

Kiến thức về hàm số: Hàm số $f\left( t \right)$ đồng biến hoặc nghịch biến trên $D$ (trong đó $D$ là một khoảng, một đoạn, một nửa khoảng) thì $u;v\in D;\,\,f\left( u \right)=f\left( v \right)\Leftrightarrow u=v$ 

Bất đẳng thức AM-GM: Cho các số thực không âm ${{a}_{1}};{{a}_{2}};...;{{a}_{n}}$ thì ta có:

${{a}_{1}}+{{a}_{2}}+...+{{a}_{n}}\ge n\sqrt[n]{{{a}_{1}}.{{a}_{2}}...{{a}_{n}}}$

Dấu bằng xảy ra $\Leftrightarrow {{a}_{1}}={{a}_{2}}=...={{a}_{n}}$ 

Bất đẳng thức Bunhiacopxki: Cho 2 bộ số thực ${{a}_{1}};{{a}_{2}};...;{{a}_{n}}$ và ${{b}_{1}};{{b}_{2}};...;{{b}_{n}}$ ta có:

$\left( a_{1}^{2}+a_{2}^{2}+...+a_{n}^{2} \right)\left( b_{1}^{2}+b_{2}^{2}+...+b_{n}^{2} \right)\ge {{\left( {{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+...+{{a}_{n}}{{b}_{n}} \right)}^{n}}$ 

Dấu bằng xảy ra $\Leftrightarrow \frac{{{a}_{1}}}{{{b}_{1}}}=\frac{{{a}_{2}}}{{{b}_{2}}}=...=\frac{{{a}_{n}}}{{{b}_{n}}}$

Bất đẳng thức trị tuyệt đối: $\left| a \right|+\left| b \right|\ge \left| a+b \right|$, dấu bằng xảy ra $\Leftrightarrow ab>0$ 

Một số bài tập trắc nghiệm giải phương trình mũ bằng cách phương pháp có đáp án chỉ tiết

Lời giải chi tiết

a) $PT\Leftrightarrow {{2}^{{{x}^{2}}-x}}+{{3}^{x-{{x}^{2}}}}+{{x}^{2}}+6={{2}^{4x-6}}+{{3}^{6-4x}}+5x\Leftrightarrow {{2}^{{{x}^{2}}-x}}+{{3}^{x-{{x}^{2}}}}+{{x}^{2}}-x={{2}^{4x-6}}+{{3}^{6-4x}}+4x-6$ 

Đặt $u={{x}^{2}}-x,\,v=4x-6$ ta có: ${{2}^{u}}-{{3}^{-u}}+u={{2}^{v}}-{{3}^{-v}}+v$ (1)

Xét hàm số: $f\left( t \right)={{2}^{t}}-{{3}^{-t}}+t\,\,\left( \forall t \right)$ ta có: ${f}'\left( t \right)={{2}^{t}}\ln 2+{{3}^{-t}}\ln 3+1>0\,\,\left( \forall t\in \mathbb{R} \right)$ 

Do đó (1) $f\left( u \right)=f\left( v \right)\Leftrightarrow u=v\Rightarrow {{x}^{2}}-x=4x-6\Leftrightarrow \left[ \begin{array}  {} x=1 \\  {} x=6 \\ \end{array} \right.$ 

Vậy phương trình có nghiệm là $x=1,x=6$.

b) Ta có: $PT\Leftrightarrow {{2}^{{{2}^{x}}}}+{{3}^{{{2}^{x}}}}+{{2}^{x}}={{2}^{x+1}}+{{3}^{x+1}}+x+1$

Xét hàm số: $f\left( t \right)={{2}^{t}}+{{3}^{t}}+t\,\,\left( \forall t\in \mathbb{R} \right)$ ta có: ${f}'\left( t \right)={{2}^{t}}\ln 2+{{3}^{t}}\ln 3+1>0\,\,\left( \forall t\in \mathbb{R} \right)$ 

Khi đó: $f\left( {{2}^{x}} \right)=f\left( x+1 \right)\Leftrightarrow {{2}^{x}}=x+1\Leftrightarrow g\left( x \right)={{2}^{x}}-x-1=0$ 

Ta có: ${g}'\left( x \right)={{2}^{x}}\ln 2-1,\,\,{{g}'}'\left( x \right)={{2}^{x}}{{\ln }^{2}}x>0\,\,\left( \forall x\in \mathbb{R} \right)$ 

Do ${{g}'}'\left( x \right)>0$ nên phương trình có tối đa 2 nghiệm, mặt khác ta thấy $g\left( 0 \right)=g\left( 1 \right)=0$ 

Vậy phương trình có nghiệm là $x=0,x=1$. 

Lời giải chi tiết

a) $PT\Leftrightarrow {{2}^{{{x}^{2}}+x}}-{{2}^{{{x}^{2}}-x+2}}-{{2}^{2x}}+{{2}^{2}}=0\Leftrightarrow {{2}^{2x}}\left( {{2}^{{{x}^{2}}-x}}-1 \right)-{{2}^{2}}\left( {{2}^{{{x}^{2}}-x}}-1 \right)=0$ 

$\Leftrightarrow \left( {{2}^{2x}}-4 \right)\left( {{2}^{{{x}^{2}}-x}}-1 \right)=0\Leftrightarrow \left[ \begin{array}  {} {{2}^{2x}}=4 \\  {} {{2}^{{{x}^{2}}-x}}=1 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}  {} x=1 \\  {} x=1,x=0 \\ \end{array} \right.$ 

Vậy phương trình có nghiệm là $x=0,x=1$. 

b) Đặt $u=2{{x}^{2}}+2x,\,v=1-{{x}^{2}}\Rightarrow PT\Leftrightarrow {{2}^{u}}+{{2}^{v}}={{2}^{u+v}}+1\Leftrightarrow \left( {{2}^{u}}-1 \right)\left( {{2}^{v}}-1 \right)=0$ 

$\Leftrightarrow \left[ \begin{array}  {} {{2}^{u}}=1 \\  {} {{2}^{v}}=1 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}  {} u=0 \\  {} v=0 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}  {} 2{{x}^{2}}+2x=0 \\  {} 1-{{x}^{2}}=0 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}  {} x=0 \\  {} x=\pm 1 \\ \end{array} \right.$ 

Vậy phương trình có nghiệm là $x=0,x=\pm 1$.

Lời giải chi tiết

a) Áp dụng BĐT: $\left| a \right|+\left| b \right|\ge \left| a+b \right|$ (dấu bằng xảy ra $\Leftrightarrow ab>0$)

Ta có: $VP=\left| {{4}^{x}}-1 \right|+\left| {{4}^{x}}-4 \right|=\left| {{4}^{x}}-1 \right|+\left| 4-{{4}^{x}} \right|\ge \left| {{4}^{x}}-1+4-{{4}^{x}} \right|=3$ 

Dấu đẳng thức xảy ra $\Leftrightarrow \left( {{4}^{x}}-1 \right)\left( 4-{{4}^{x}} \right)\ge 0$ 

Mặt khác ta có: $-{{x}^{2}}+x+\frac{11}{4}=3-{{\left( x-\frac{1}{2} \right)}^{2}}\le 3\le \text{VT}\Rightarrow \text{VT=VP}\Leftrightarrow x=\frac{1}{2}$

Vậy $x=\frac{1}{2}$ là nghiệm duy nhất của phương trình đã cho.

b) Áp dụng BĐT AM-GM ta có: $VP={{3}^{x}}+\frac{1}{{{3}^{x}}}\ge 2\sqrt{{{3}^{x}}.\frac{1}{{{3}^{x}}}}=2\ge 2co{{s}^{2}}\left( \frac{{{x}^{3}}-x}{2} \right)=VT$ 

Dấu đẳng thức xảy ra $\Leftrightarrow \left\{ \begin{array}  {} {{3}^{x}}=\frac{1}{{{3}^{x}}} \\  {} co{{s}^{2}}\left( \frac{{{x}^{3}}-x}{2} \right)=1 \\ \end{array} \right.\Leftrightarrow \left[ \begin{array}  {} x=0 \\  {} co{{s}^{2}}\left( \frac{{{x}^{3}}-x}{2} \right)=1 \\ \end{array} \right.\Leftrightarrow x=0$ 

Vậy $x=0$ là nghiệm duy nhất của phương trình đã cho.

Lời giải chi tiết

a) Đặt $t={{3}^{{{x}^{2}}}}>0$ ta có: ${{t}^{2}}+\left( {{x}^{2}}-3 \right)t-2{{x}^{2}}+2=0$ 

Khi đó: $\Delta ={{\left( {{x}^{2}}-3 \right)}^{2}}-4\left( -2{{x}^{2}}+2 \right)={{x}^{4}}+2{{x}^{2}}+1={{\left( {{x}^{2}}+1 \right)}^{2}}$ 

Do đó: $\left[ \begin{array}  {} t=\frac{3-{{x}^{2}}+{{x}^{2}}+1}{2}=2 \\  {} t=\frac{3-{{x}^{2}}-\left( {{x}^{2}}+1 \right)}{2}=1-{{x}^{2}} \\ \end{array} \right.$ 

Với $t=2\Leftrightarrow {{3}^{{{x}^{2}}}}=2\Leftrightarrow x=\pm \sqrt{{{\log }_{3}}2}$ 

Với $t=1\Leftrightarrow {{3}^{{{x}^{2}}}}=1-{{x}^{2}}$. Ta có: $VT={{3}^{{{x}^{2}}}}\ge {{3}^{0}}=1\ge VP$ nên $VT=VP\Leftrightarrow x=0$ 

Vậy nghiệm của phương trình là: $x=0,x=\pm \sqrt{{{\log }_{3}}2}$ 

b) $PT\Leftrightarrow 2{{x}^{2}}-3\left( 1-{{4.3}^{x}} \right)x-{{6.3}^{x}}+1=0$ 

Khi đó: $\Delta =9\left( 1-{{8.3}^{x}}+{{16.9}^{x}} \right)-8\left( -{{6.3}^{x}}+1 \right)={{144.9}^{x}}-{{24.3}^{x}}+1={{\left( {{12.3}^{x}}-1 \right)}^{2}}$ 

Do vậy $\left\{ \begin{array}  {} x=\frac{3-{{2.3}^{x}}+{{12.3}^{x}}-1}{4}=\frac{1}{2} \\  {} x=\frac{3-{{12.3}^{x}}-{{12.3}^{x}}+1}{4}=1-{{6.3}^{x}}\,\,\left( 2 \right) \\ \end{array} \right.$ 

(2) $\Leftrightarrow g\left( x \right)=x+{{6.3}^{x}}-1=0\,\,$ (3)

Ta có: ${g}'\left( x \right)=1+{{6.3}^{x}}\ln 3>0$ $\left( \forall x\in \mathbb{R} \right)$ 

Do dó hàm số $g\left( x \right)$ đồng biến trên $\mathbb{R}$ ta có: (3) $g\left( x \right)=g\left( -1 \right)\Leftrightarrow x=-1$ 

Vậy phương trình đã cho có 2 nghiệm $x=\frac{1}{2},\,x=-1$ 

Lời giải chi tiết

Xét hàm số $f\left( x \right)={{7}^{x}}-6x-1$ trên tập $\mathbb{R}$ ta có: ${f}'\left( x \right)={{7}^{x}}\ln 7-6=0\Leftrightarrow x={{\log }_{7}}\frac{6}{\ln 7}={{x}_{0}}$              

Lại có: $\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=+\infty $ và $f\left( {{x}_{0}} \right)=f\left( {{\log }_{7}}\frac{6}{\ln 7} \right)<0$ 

Suy ra BBT:

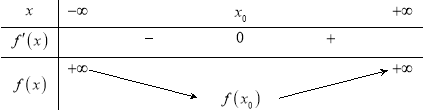
Do đó phương trình đã cho có 2 nghiệm. Chọn C.

Lời giải chi tiết

Ta có: $PT\Leftrightarrow {{2}^{x-1}}+x-1={{2}^{{{x}^{2}}-x}}+{{x}^{2}}-x$ (*)

Xét hàm số $f\left( t \right)={{2}^{t}}+t\Rightarrow {f}'\left( t \right)={{2}^{t}}\ln 2+1>0\,\,\left( \forall t\in \mathbb{R} \right)\Rightarrow f\left( t \right)$ là hàm đồng biến trên $\mathbb{R}$

Khi đó (*) $\Leftrightarrow f\left( x-1 \right)=f\left( {{x}^{2}}-x \right)\Leftrightarrow x-1={{x}^{2}}-x\Leftrightarrow x=1$. Chọn B.

Lời giải chi tiết

Ta có: $PT\Leftrightarrow {{2}^{{{x}^{2}}-3x+1}}+{{x}^{2}}-3x+1={{2}^{x-2}}+x-2$ (*)

Xét hàm số $f\left( t \right)={{2}^{t}}+t\Rightarrow {f}'\left( t \right)={{2}^{t}}\ln 2+1>0\,\,\left( \forall t\in \mathbb{R} \right)\Rightarrow f\left( t \right)$ là hàm đồng biến trên $\mathbb{R}$

Khi đó (*) $\Leftrightarrow f\left( {{x}^{2}}-3x+1 \right)=f\left( x-2 \right)\Leftrightarrow {{x}^{2}}-3x+1=x-2\Leftrightarrow {{x}^{2}}-4x+3\Leftrightarrow \left[ \begin{array}  {} x=1 \\  {} x=3 \\ \end{array} \right.$. Chọn C.

Lời giải chi tiết

ĐK: $x\ne 0$. Khi đó $PT\Leftrightarrow {{2}^{\frac{1}{{{x}^{2}}}-1}}-{{2}^{\frac{1}{{{x}^{2}}}-\frac{2}{x}}}=\frac{1}{2}-\frac{1}{x}$ 

$\Leftrightarrow {{2}^{\frac{1}{{{x}^{2}}}-1}}+\frac{1}{2}\left( \frac{1}{{{x}^{2}}}-1 \right)={{2}^{\frac{1}{{{x}^{2}}}-\frac{2}{x}}}+\frac{1}{2}\left( \frac{1}{{{x}^{2}}}-\frac{2}{x} \right)$

Xét hàm số $f\left( t \right)={{2}^{t}}+\frac{1}{2}t\Rightarrow {f}'\left( t \right)={{2}^{t}}\ln 2+\frac{1}{2}>0\,\,\left( \forall t\in \mathbb{R} \right)\Rightarrow f\left( t \right)$ là hàm đồng biến trên $\mathbb{R}$ 

Khi đó (*) $\Leftrightarrow f\left( \frac{1}{{{x}^{2}}}-1 \right)=f\left( \frac{1}{{{x}^{2}}}-\frac{1}{x} \right)\Leftrightarrow \frac{1}{{{x}^{2}}}-1=\frac{1}{{{x}^{2}}}-\frac{1}{x}\Leftrightarrow -1=-\frac{1}{x}\Leftrightarrow x=1$. Chọn B.