Toggle Mobile Menu
Xét các số thực không âm a, b ,c thỏa mãn a + b + c = 1. Tìm

Câu hỏi và phương pháp giải
Nhận biếtXét các số thực không âm a, b ,c thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức M = ab + bc + ca – 2abc.
Đáp án đúng: A
Lời giải của Luyện Tập 247
Lời giải chi tiết:
Ta có ab + bc + ca – 2abc = a(b + c) + (1 – 2a)bc = a(1 – a) + (1 – 2a)bc
Đặt t = bc thì ta có 0 ≤ t = bc ≤ 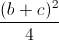 =
=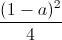
Xét hs f(t) = a(1 – a) + (1 – 2a)t là đơn điệu trên đoạn [0; 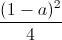 ]
]
Có f(0) = a(1 – a) ≤ 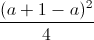 =
=  <
< 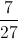 và f(
và f(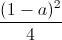 ) =
) =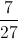 -
-  (2a +
(2a +  )(a -
)(a -  )2 ≤
)2 ≤ 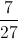 với mọi a ∈[0;1]
với mọi a ∈[0;1]
Vậy ab + bc + ca – 2abc ≤ 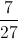 .Đẳng thức xảy ra khi a = b =c =
.Đẳng thức xảy ra khi a = b =c = 
Max M = 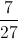 .
.
( * ) Xem thêm: Ôn tập luyện thi thpt quốc gia môn toán cơ bản và nâng cao. Tổng hợp đầy đủ lý thuyết, công thức, phương pháp giải và bài tập vận dụng.